The Facility Layout Planning Problem#
Optimization Model for Facility Layout Planning
A facility layout problem involves determining the optimal arrangement of physical spaces and resources within a facility to achieve maximum efficiency, productivity, and safety. This problem is common in various types of facilities such as manufacturing plants, warehouses, hospitals, offices, and retail stores. The goal is to minimize costs associated with material handling, labor, and space while ensuring a smooth workflow and meeting operational requirements.
Problem Definition
The task involves designing the layout for a new manufacturing plant. This plant will consist of several stations, each with specific functions and space requirements. The primary objectives are to minimize material handling costs, optimize workflow efficiency, and ensure compliance with safety and ergonomic standards.
The facility’s size will be determined based on the placement of the stations and it should be minimized. When constructing the facility, it’s crucial to place stations with adequate pathways between them, maintaining a constant amount of empty space around each station.
The facility should also include a Receiving area at the bottom and a Storage area at the top of the layout, ensuring that all materials complete the workflow process before reaching the Storage area.
Additionally, an administrative office should be positioned near the center of the facility, ideally in a central location.
Material handling costs vary between stations and must be minimized, considering that material flow can occur between any stations.
Libraries
To begin, we install and import the necessary libraries.
pip install quantagonia
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from pulp import *
from quantagonia import HybridSolverParameters
import quantagonia.mip.pulp_adapter as pulp_adapter
API_KEY= "Your-API-KEY" # if you don't have one, head over to https://platform.quantagonia.com/
Problem Parameters
NumStations: Number of stations to be placed
PathwaySize: Pathway length and width
BIG_M: Artificial big number
WidthStation\(_{i}\): Width of the station \(i\)
LengthStation\(_{i}\): Length of the station \(i\)
PairwiseCost\(_{i,j}\): Material handling cost between every station(inculing receiving and storage area; excluding admin area)
# PARAMETERS
NUM_STATIONS = 7 # Number of stations
NUM_STATIONS = NUM_STATIONS + 3 # (+3 is for receiving, storage areas and admin office)
BIG_M = 50 #Artificial big number.
PATHWAY_SIZE = 2 # Pathway length and width
##Randomly assign the dimensions of the stations
np.random.seed(1)
WIDTH_STATION = np.random.randint(1.5, 5, size=(NUM_STATIONS))
LENGTH_STATION = np.random.randint(1.5, 5, size=(NUM_STATIONS))
## Change the sizes of the special areas.
# Assuming that station 0 is Receiving Area, Station 1 is Storage Area, Station 2 is Admin Office
RECEIVING_AREA_WIDTH= 4;RECEIVING_AREA_LENGTH = 2
STORAGE_AREA_WIDTH= 4;STORAGE_AREA_LENGTH = 2
ADMIN_OFFICE_WIDTH = 3;ADMIN_OFFICE_LENGTH = 3
WIDTH_STATION[0] = RECEIVING_AREA_WIDTH;WIDTH_STATION[1] = STORAGE_AREA_WIDTH;WIDTH_STATION[2] = ADMIN_OFFICE_WIDTH
LENGTH_STATION[0] = RECEIVING_AREA_LENGTH;LENGTH_STATION[1] = STORAGE_AREA_LENGTH;LENGTH_STATION[2] = ADMIN_OFFICE_LENGTH
### Randomly decide pairwise material handling cost between every station (inculing receiving and storage area; excluding admin area)
PAIRWISE_COST = np.random.randint(1, 20, size=(NUM_STATIONS,NUM_STATIONS))
PAIRWISE_COST = (PAIRWISE_COST + PAIRWISE_COST.T)/2 # Turn the pairwise matrix into a symmetric matrix
PAIRWISE_COST[:,2] = 0; PAIRWISE_COST[2,:] = 0
for i in range(NUM_STATIONS): PAIRWISE_COST[i,i] = 0
Sets and Indices
\(i,j \in S = {0,1,..,NumStation}\) : Workstation Indices
# SETS
station_set = list(range(NUM_STATIONS)) ## Station Indices #i,j
Decision Variables
\(length \in \mathbb{R}^+\): The length of the whole layout.
\(width \in \mathbb{R}^+\): The width of the whole layout.
\(x_{i} \in \mathbb{R}^+\): The horizontal position of the station i.
\(y_{i} \in \mathbb{R}^+\): The vertical position of the station i.
\(dx_{i,j} \in \mathbb{R}^+\): Sum of absolute horizontal differences between every robot.
\(dy_{i,j} \in \mathbb{R}^+\): Sum of absolute vertical differences between every robot.
\(isright_{i, j} \in \{0, 1\}\): If unit i is completely on the RIGHT side of j, it is 1; otherwise 0.
\(isleft_{i, j} \in \{0, 1\}\): If unit i is completely on the LEFT side of j, it is 1; otherwise 0.
\(isbelow_{i, j} \in \{0, 1\}\): If unit i is completely on the BELOW side of j, it is 1; otherwise 0.
\(isabove_{i, j} \in \{0, 1\}\): If unit i is completely on the ABOVE side of j, it is 1; otherwise 0.
#DECISION VARIABLES
### Continuous --> The length of the whole layout.
length = LpVariable(name = 'length', lowBound = 0, cat='Continuous')
### Continuous --> The width of the whole layout.
width = LpVariable(name = 'width', lowBound = 0, cat='Continuous')
### Continuous --> The horizontal position of the station i.
x = []
for i in station_set:
x.append(LpVariable(name = 'x_coordinate_station(%d)' % (i), lowBound = 0, cat='Continuous'))
### Continuous --> The vertical position of the station i.
y = []
for i in station_set:
y.append(LpVariable(name = 'y_coordinate_station(%d)' % (i), lowBound = 0, cat='Continuous'))
### Continuous --> Sum of absolute horizontal differences between every robot.
dx = []
for i in station_set:
dx.append([])
for j in station_set:
dx[i].append(LpVariable(name = 'x_distance_between(%d,%d)' % (i,j), lowBound = 0, cat='Continuous'))
### Continuous --> Sum of absolute vertical differences between every robot.
dy = []
for i in station_set:
dy.append([])
for j in station_set:
dy[i].append(LpVariable(name = 'y_distance_between(%d,%d)' % (i,j), lowBound = 0, cat='Continuous'))
### BINARY --> If station i is completely on the RIGHT side of j, it is 1; otherwise 0.
isright = []
for i in station_set:
isright.append([])
for j in station_set:
isright[i].append(LpVariable(name = 'isright(%d,%d)' % (i,j), cat='Binary'))
### BINARY --> If station i is completely on the LEFT of j, it is 1; otherwise 0
isleft = []
for i in station_set:
isleft.append([])
for j in station_set:
isleft[i].append(LpVariable(name = 'isleft(%d,%d)' % (i,j), cat='Binary'))
### BINARY --> If station i is completely on the BELOW of j, it is 1; otherwise 0
isbelow = []
for i in station_set:
isbelow.append([])
for j in station_set:
isbelow[i].append(LpVariable(name = 'isbelow(%d,%d)' % (i,j), cat='Binary'))
### BINARY --> If station i is completely on the ABOVE of j, it is 1; otherwise 0
isabove = []
for i in station_set:
isabove.append([])
for j in station_set:
isabove[i].append(LpVariable(name = 'isabove(%d,%d)' % (i,j), cat='Binary'))
Objective Function
The objective function is minimizing L1(Manhattan) Distances between all the stations while simultaneously minimize the overall size of the facility.
prob = LpProblem("Facility_Layout", LpMinimize)
### OBJECTIVE FUNCTION
prob += (lpSum((dx[i][j] + dy[i][j]) * PAIRWISE_COST[i,j] for i in station_set for j in range(i+1,NUM_STATIONS))
+ (length + width) * (PAIRWISE_COST.sum()/2))
Constraints
Constraints 1:
Every unit (Stations, Receiving Area, Storage Area and Admin Office) must be located within the facility boundaries.
Constraints 2:
Non Overlaping Constraints Between Every Units (Stations, Receiving Area, Storage Area and Admin office)
Constraint 3:
Each unit (robots and stations) has to be completely on at least one side of another unit.
Constraints 4:
Calculate the absolute horizontal and vertical distances between every robots.
Constraints 5:
Fix the positions of the receiving and storage areas to the bottom and top respectively.
Assuming that station 0 is Receiving Area and station 1 is Storage Area
Constraints 6:
Admin office should be centerally located.
Assuming that Station 2 is Admin Office
### CONSTRAINTS
## Constraints 1: Stations must be located within the facility boundaries.
for i in station_set:
prob += (x[i] <= width - WIDTH_STATION[i], f"Constraint1a_{i}")
prob += (y[i] <= length - LENGTH_STATION[i], f"Constraint1b_{i}")
## Constraints 2: Non Overlaping Constraints Between Units(Stations, Receiving Area, Storage Area and Admin office)
for i in station_set:
for j in station_set:
if j>i:
prob += (y[j] - y[i] >= isbelow[i][j] * LENGTH_STATION[i] + PATHWAY_SIZE - (BIG_M * (1-isbelow[i][j])), f"Constraint2_a{i,j}")
prob += (y[i] - y[j] >= isabove[i][j] * LENGTH_STATION[j] + PATHWAY_SIZE - (BIG_M * (1-isabove[i][j])), f"Constraint2_b{i,j}")
prob += (x[j] - x[i] >= isleft[i][j] * WIDTH_STATION[i] + PATHWAY_SIZE - (BIG_M * (1-isleft[i][j])), f"Constraint2_c{i,j}")
prob += (x[i] - x[j] >= isright[i][j] * WIDTH_STATION[j] + PATHWAY_SIZE - (BIG_M * (1-isright[i][j])), f"Constraint2_d{i,j}")
## Constraint 3: Each unit has to be completely on at least one side of another Units(Stations, Receiving Area, Storage Area and Admin office).
for i in station_set:
for j in station_set:
if j>i:
prob += (isbelow[i][j]+isabove[i][j]+isleft[i][j]+isright[i][j] >= 1, f"Constraint3{i,j}")
## Constraint 4: Calculate the absolute horizontal and vertical distances between every Units(Stations, Receiving Area, Storage Area and Admin office).
for i in station_set:
for j in station_set:
if j>i:
prob += (dx[i][j] >= (x[i] - x[j]), f"Constraint4a_{i,j}")
prob += (dx[i][j] >= (x[j] - x[i]), f"Constraint4b_{i,j}")
prob += (dy[i][j] >= (y[i] - y[j]), f"Constraint4c_{i,j}")
prob += (dy[i][j] >= (y[j] - y[i]), f"Constraint4d_{i,j}")
## Constraints 5: Fix the positions of the receiving and storage areas to the bottom and top respectively.
# Assuming that station 0 is Receiving Area, station 1 is Storage Area, station 2 is Admin Office
prob += (y[0] == 0, f"Constraint5_{0}")
prob += (y[1] == length-LENGTH_STATION[1], f"Constraint5_{2}")
## Constraints 6: Admin office should be centerally located
# Assuming that Station 2 is Admin Office
prob += (x[2] == (width*0.5) - WIDTH_STATION[2]/2, f"Constraint6_{3}")
prob += (y[2] == (length*0.5) - LENGTH_STATION[2]/2, f"Constraint6_{4}")
params = HybridSolverParameters()
params.set_time_limit(900)
params.set_seed(0)
params.set_relative_gap(0.1)
q_solver = pulp_adapter.HybridSolver_CMD(api_key=API_KEY, params=params)
status = prob.solve(solver=q_solver)
print("Status:",LpStatus[status],"\nObjective Function Value: %.2f"%prob.objective.value())
✔ Queued job with jobid 25ad95c3-abe1-4c01-9477-952d419245af...
✔ Job 25ad95c3-abe1-4c01-9477-952d419245af unqueued, processing...
Quantagonia HybridSolver version 1.1.1909
Copyright (c) 2024 Quantagonia GmbH.
User-specified parameters:
Set parameter 'time_limit' to value '900.0'.
Set parameter 'seed' to value '0'.
Set parameter 'relative_gap' to value '0.1'.
Read 89024223d7934c8581005e5098d8defa-pulp.mps in 0.62s.
Minimize a MILP with 429 constraints and 292 variables (180 binary, 0 integer, 0 implied integer, 112 continuous).
Presolving model. Presolved model in 0.01s.
Reduced model has 359 constraints and 252 variables (170 binary, 0 integer, 82 continuous).
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
1 | inf | 0.00000000 | inf | 0.01 |
* 1 | 17498.5000 | 6720.40851 | 61.59 | 0.01 |
166 | 17498.5000 | 7751.64482 | 55.70 | 1.14 |
* 178 | 14503.0000 | 7751.64482 | 46.55 | 1.34 |
* 350 | 13687.0000 | 8003.57156 | 41.52 | 2.40 |
560 | 13687.0000 | 8184.01865 | 40.21 | 3.82 |
740 | 13687.0000 | 8330.51775 | 39.14 | 4.92 |
937 | 13687.0000 | 8392.34941 | 38.68 | 5.98 |
1155 | 13687.0000 | 8472.80403 | 38.10 | 7.13 |
1331 | 13687.0000 | 8519.57402 | 37.75 | 8.31 |
1476 | 13687.0000 | 8728.15048 | 36.23 | 9.38 |
1613 | 13687.0000 | 8917.27003 | 34.85 | 10.38 |
1825 | 13687.0000 | 9057.70136 | 33.82 | 11.46 |
2065 | 13687.0000 | 9713.58105 | 29.03 | 12.59 |
2286 | 13687.0000 | 10028.0549 | 26.73 | 13.79 |
2545 | 13687.0000 | 10222.7905 | 25.31 | 14.87 |
2788 | 13687.0000 | 10423.6717 | 23.84 | 16.01 |
2968 | 13687.0000 | 10457.7366 | 23.59 | 17.10 |
3230 | 13687.0000 | 10516.7772 | 23.16 | 18.10 |
3407 | 13687.0000 | 10556.6918 | 22.87 | 19.17 |
3700 | 13687.0000 | 10676.2513 | 22.00 | 20.26 |
3936 | 13687.0000 | 10701.9819 | 21.81 | 21.37 |
4208 | 13687.0000 | 10748.6101 | 21.47 | 22.43 |
4389 | 13687.0000 | 10805.4728 | 21.05 | 23.47 |
4664 | 13687.0000 | 10878.1217 | 20.52 | 24.60 |
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
4933 | 13687.0000 | 10929.4479 | 20.15 | 25.82 |
5193 | 13687.0000 | 10947.3469 | 20.02 | 27.16 |
5490 | 13687.0000 | 10959.7628 | 19.93 | 28.37 |
5690 | 13687.0000 | 10971.0906 | 19.84 | 29.58 |
5929 | 13687.0000 | 10987.3113 | 19.72 | 30.66 |
6245 | 13687.0000 | 11004.9709 | 19.60 | 31.81 |
6482 | 13687.0000 | 11014.7976 | 19.52 | 32.92 |
6699 | 13687.0000 | 11027.4580 | 19.43 | 34.06 |
6907 | 13687.0000 | 11047.2281 | 19.29 | 35.37 |
7242 | 13687.0000 | 11063.2226 | 19.17 | 36.65 |
7515 | 13687.0000 | 11077.7061 | 19.06 | 37.96 |
7840 | 13687.0000 | 11087.4268 | 18.99 | 39.08 |
8079 | 13687.0000 | 11108.6123 | 18.84 | 40.10 |
8325 | 13687.0000 | 11137.6829 | 18.63 | 41.34 |
8513 | 13687.0000 | 11160.5548 | 18.46 | 42.46 |
8788 | 13687.0000 | 11178.1303 | 18.33 | 43.78 |
9110 | 13687.0000 | 11209.2493 | 18.10 | 44.87 |
9297 | 13687.0000 | 11227.7833 | 17.97 | 46.05 |
9585 | 13687.0000 | 11270.9390 | 17.65 | 47.13 |
9781 | 13687.0000 | 11288.5362 | 17.52 | 48.19 |
10048 | 13687.0000 | 11332.0583 | 17.21 | 49.23 |
10302 | 13687.0000 | 11356.7984 | 17.02 | 50.34 |
10528 | 13687.0000 | 11393.8983 | 16.75 | 51.64 |
10704 | 13687.0000 | 11409.1516 | 16.64 | 52.68 |
10979 | 13687.0000 | 11423.1273 | 16.54 | 53.86 |
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
11309 | 13687.0000 | 11453.2319 | 16.32 | 55.12 |
11518 | 13687.0000 | 11466.2954 | 16.22 | 56.30 |
11841 | 13687.0000 | 11504.5355 | 15.95 | 57.64 |
12048 | 13687.0000 | 11512.8929 | 15.88 | 58.88 |
12268 | 13687.0000 | 11521.3748 | 15.82 | 59.96 |
12500 | 13687.0000 | 11531.1611 | 15.75 | 60.97 |
12697 | 13687.0000 | 11538.6842 | 15.70 | 62.08 |
12953 | 13687.0000 | 11551.3085 | 15.60 | 63.20 |
13221 | 13687.0000 | 11575.0913 | 15.43 | 64.27 |
13505 | 13687.0000 | 11594.5838 | 15.29 | 65.99 |
13802 | 13687.0000 | 11611.1537 | 15.17 | 67.18 |
14039 | 13687.0000 | 11619.7326 | 15.10 | 68.32 |
14368 | 13687.0000 | 11634.0623 | 15.00 | 69.43 |
14621 | 13687.0000 | 11642.5866 | 14.94 | 70.56 |
14797 | 13687.0000 | 11654.6259 | 14.85 | 71.57 |
15045 | 13687.0000 | 11672.2749 | 14.72 | 72.72 |
15261 | 13687.0000 | 11678.3290 | 14.68 | 73.90 |
* 15543 | 13686.5000 | 11693.0280 | 14.57 | 74.79 |
* 15543 | 13680.5000 | 11693.0280 | 14.53 | 74.93 |
15715 | 13680.5000 | 11698.0292 | 14.49 | 76.31 |
* 15863 | 13334.0000 | 11705.2365 | 12.22 | 76.43 |
16005 | 13334.0000 | 11710.7287 | 12.17 | 77.61 |
16317 | 13334.0000 | 11733.5218 | 12.00 | 78.64 |
16402 | 13334.0000 | 11734.2747 | 12.00 | 79.94 |
16822 | 13334.0000 | 11750.7280 | 11.87 | 81.29 |
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
17028 | 13334.0000 | 11759.8214 | 11.81 | 82.30 |
17284 | 13334.0000 | 11764.5712 | 11.77 | 83.38 |
17538 | 13334.0000 | 11770.1983 | 11.73 | 84.55 |
17835 | 13334.0000 | 11777.8376 | 11.67 | 85.60 |
18083 | 13334.0000 | 11789.2943 | 11.58 | 86.80 |
18406 | 13334.0000 | 11811.7214 | 11.42 | 87.95 |
18487 | 13334.0000 | 11815.2986 | 11.39 | 89.23 |
18883 | 13334.0000 | 11827.8488 | 11.30 | 90.68 |
19310 | 13334.0000 | 11839.6072 | 11.21 | 91.86 |
19422 | 13334.0000 | 11844.7650 | 11.17 | 92.93 |
19666 | 13334.0000 | 11854.3891 | 11.10 | 93.95 |
20015 | 13334.0000 | 11867.5937 | 11.00 | 95.00 |
20199 | 13334.0000 | 11870.7873 | 10.97 | 96.65 |
20559 | 13334.0000 | 11882.8504 | 10.88 | 98.04 |
20950 | 13334.0000 | 11894.7171 | 10.79 | 99.48 |
21236 | 13334.0000 | 11908.2793 | 10.69 | 100.57 |
21422 | 13334.0000 | 11911.5288 | 10.67 | 102.61 |
21959 | 13334.0000 | 11928.7440 | 10.54 | 103.82 |
22146 | 13334.0000 | 11931.5713 | 10.52 | 105.56 |
22632 | 13334.0000 | 11942.4046 | 10.44 | 107.77 |
22981 | 13334.0000 | 11949.5374 | 10.38 | 108.85 |
23370 | 13334.0000 | 11963.5842 | 10.28 | 110.13 |
23562 | 13334.0000 | 12000.6856 | 10.00 | 110.63 |
------------------------------------------------------------------------
Optimal solution found (within relative tolerance 10.0%).
Solver Results:
- Solution Status: Optimal
- Wall Time: 110.6336 seconds
- Objective: 13334.0000
- Bound: 12000.6856
- Absolute Gap: 1333.3144
- Relative Gap: 9.9994%
- Nodes: 23562
- Best solution found at node 15863 after 76.4345 seconds
Finished processing job 25ad95c3-abe1-4c01-9477-952d419245af...
Optimal
Status: Optimal
Objective Function Value: 13334.00
Creating the Outputs of the Solution
resultx = np.zeros((NUM_STATIONS))
resulty = np.zeros((NUM_STATIONS))
resultdx = np.zeros((NUM_STATIONS,NUM_STATIONS))
resultdy = np.zeros((NUM_STATIONS,NUM_STATIONS))
result_isright = np.zeros((NUM_STATIONS,NUM_STATIONS))
result_isleft = np.zeros((NUM_STATIONS,NUM_STATIONS))
result_istop = np.zeros((NUM_STATIONS,NUM_STATIONS))
result_isbelow = np.zeros((NUM_STATIONS,NUM_STATIONS))
maintenance_schedule_df = pd.DataFrame(columns = ['Powerplant_Id','Week_Id','Status'])
for i in station_set:
resultx[i]=(x[i].varValue)
resulty[i]=(y[i].varValue)
for i in station_set:
for j in station_set:
resultdx[i,j]=(dx[i][j].varValue)
resultdy[i,j]=(dy[i][j].varValue)
result_isright[i,j]=(isright[i][j].varValue)
result_isleft[i,j]=(isleft[i][j].varValue)
result_istop[i,j]=(isabove[i][j].varValue)
result_isbelow[i,j]=(isbelow[i][j].varValue)
Visualize the Layout
# Generate random colors for each rectangle
colors = np.random.rand(len(resultx))
colors = np.random.uniform(low=0, high=1, size=len(resultx))
# Create figure and axes
fig, ax = plt.subplots(figsize=((width.varValue/length.varValue*10), (length.varValue/width.varValue*10)))
# Set the background color of the layout area only
background_rect = patches.FancyBboxPatch(
(-.5, -.5), width.varValue +1, length.varValue+1,
boxstyle="round,pad=0,rounding_size=0",
facecolor='lightgrey',
edgecolor='none',
zorder=-1
)
ax.add_patch(background_rect)
# Plot rectangles with rounded edges
for i in range(len(resultx)):
if i in [0, 1, 2]:
rect = patches.FancyBboxPatch(
(resultx[i], resulty[i]),
WIDTH_STATION[i],
LENGTH_STATION[i],
boxstyle="round,pad=0.1",
color='grey',
edgecolor='black',
linewidth=4,
linestyle='--'
)
ax.add_patch(rect)
else:
rect = patches.FancyBboxPatch(
(resultx[i], resulty[i]),
WIDTH_STATION[i],
LENGTH_STATION[i],
boxstyle="round,pad=0.1",
color=plt.cm.viridis(colors[i]),
edgecolor='black',
linewidth=4,
linestyle='-'
)
ax.add_patch(rect)
# Labels
# Assumed that station 0 is Receiving Area, Station 1 is Storage Area, Station 2 is Admin Office
if i == 0:
plt.text(resultx[i] + WIDTH_STATION[i]/2, resulty[i] + LENGTH_STATION[i]/2, str('Receiving Area ' + str(i + 1)), color='black', ha='center', va='center', fontsize=15)
elif i == 1:
plt.text(resultx[i] + WIDTH_STATION[i]/2, resulty[i] + LENGTH_STATION[i]/2, str('Storage Area ' + str(i + 1)), color='black', ha='center', va='center', fontsize=15)
elif i == 2:
plt.text(resultx[i] + WIDTH_STATION[i]/2, resulty[i] + LENGTH_STATION[i]/2, 'Admin Office', color='black', ha='center', va='center', fontsize=15)
else:
plt.text(resultx[i] + WIDTH_STATION[i]/2, resulty[i] + LENGTH_STATION[i]/2, str('Station ' + str(station_set[i] - 2)), color='black', ha='center', va='center', fontsize=15)
# Add titles and labels
plt.title('Layout Plan', fontsize=25)
plt.xlabel('Horizontal Axis(x)')
plt.ylabel('Vertical Axis(y)')
# Specify x and y limits
plt.xlim(-.5, width.varValue + .5)
plt.ylim(-.5, length.varValue + .5)
# Add legend
legend_elements = [
patches.Patch(facecolor='grey', edgecolor='black', linestyle='--', linewidth=1, label='Special Areas (Receiving, Storage, Admin)'),
patches.Patch(facecolor=plt.cm.viridis(0.5), edgecolor='black', linewidth=1, label='Stations')
]
ax.legend(handles=legend_elements, loc='upper left')
# Show plot
plt.grid(False)
plt.show()
Setting the 'color' property will override the edgecolor or facecolor properties.
Setting the 'color' property will override the edgecolor or facecolor properties.
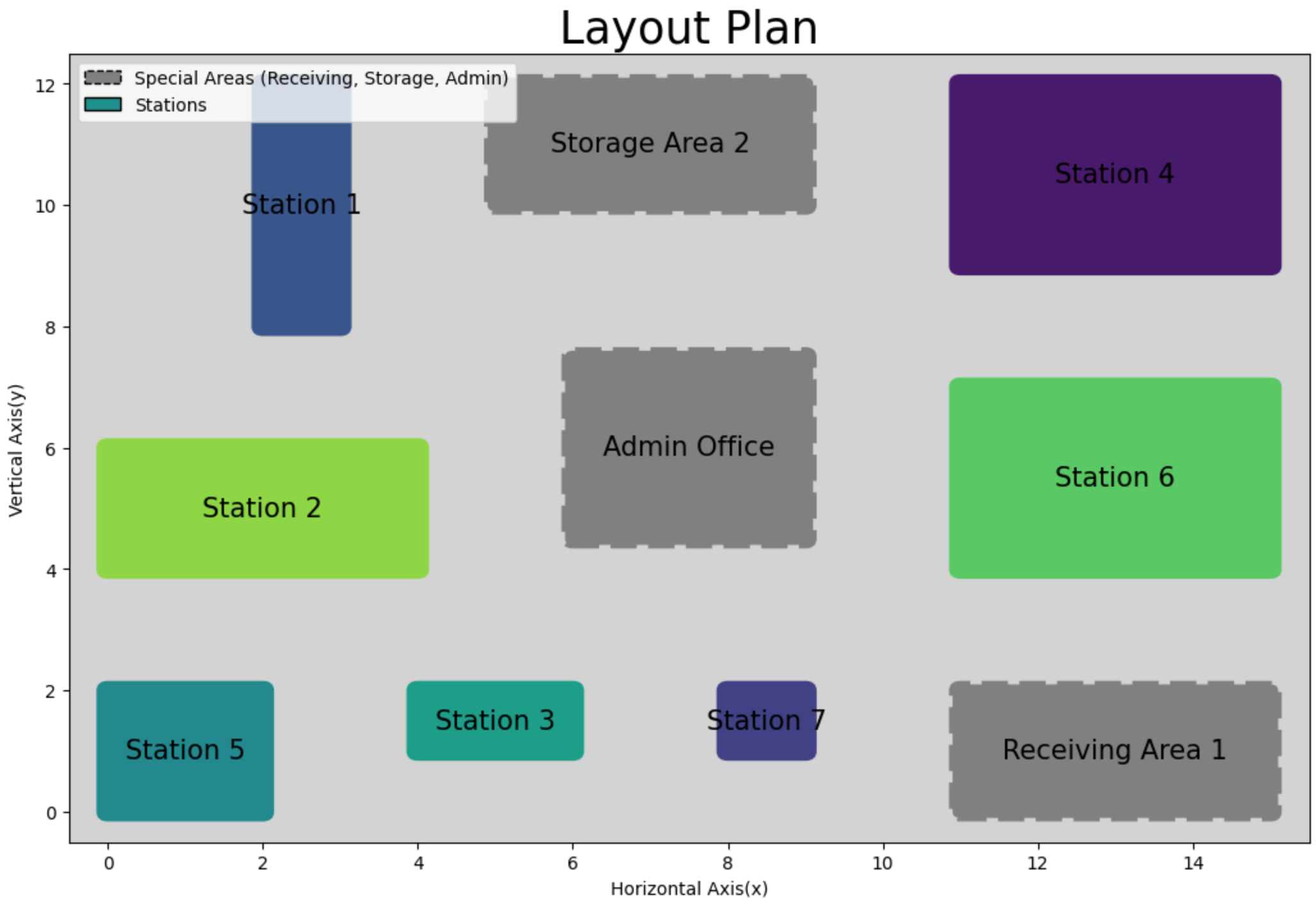
Conclusion:
The layout plan for the new manufacturing plant, as depicted in the provided image, successfully arranges the stations and special areas (Receiving, Storage, and Admin Office) to meet the project’s primary objectives. The stations are strategically placed to minimize total layout area, material handling costs, optimize workflow efficiency, and adhere to safety and ergonomic standards. The Admin Office is centrally located to facilitate easy management access, while the Receiving and Storage areas are positioned at the bottom and top, respectively, to streamline material flow throughout the facility.
To further develop any layout, it is essential to conduct a detailed workflow analysis to identify potential bottlenecks, use simulation software to test the layout under various scenarios, and perform a safety and ergonomic assessment to ensure compliance with industry standards.
Need help with modeling? We are happy to coach you through your model formulation. Reach out to us at help@quantagonia.com or https://www.quantagonia.com/contact.
## References
Alejo, J. S., Martín, M. G., Ortega-Mier, M., & García-Sánchez, A. (2009). Mixed integer programming model for optimizing the layout of an ICU vehicle. BMC Health Services Research, 9(1). https://doi.org/10.1186/1472-6963-9-224
Anjos, M. F., & Vieira, M. V. C. (2020). Mathematical optimization approach for facility layout on several rows. Optimization Letters, 15(1), 9–23. https://doi.org/10.1007/s11590-020-01621-z
Braga, E. M. H., & De Salles Neto, L. L. (2022). A MATHEMATICAL OPTIMIZATION APPROACH BASED ON LINEARIZED MIP MODELS FOR SOLVING FACILITY LAYOUT PROBLEMS. Pesquisa Operacional, 42. https://doi.org/10.1590/0101-7438.2022.042.00261044
Drira, A., Pierreval, H., & Hajri-Gabouj, S. (2006). FACILITY LAYOUT PROBLEMS: A LITERATURE ANALYSIS. IFAC Proceedings Volumes, 39(3), 389–400. https://doi.org/10.3182/20060517-3-fr-2903.00208