The Maintenance Scheduling Problem#
Optimization Model for Maintenance Scheduling
The maintenance scheduling problem is a critical challenge faced by the electric power industry, particularly in the management of power generating units. At its core, it involves efficiently scheduling maintenance for power generating units while considering constraints and objective. These constraints may include specific needs based on type of the operation.
Problem Definition
This example focuses on maintenance scheduling problem in the electric power industry by developing and solving a mathematical model to optimize operations. The primary objective is to minimize the total operating costs while determining the schedule for maintenance of power plant units and meeting power demand in a given planning horizon.
Each power plant unit can be in one of three states during a particular week: ON, OFF, or MAINTENANCE. The operating and maintenance costs vary depending on the week. If a power plant unit does not operate during a week, no costs are incurred.
Several constraints must be considered, including the maximum number of units that can be under maintenance simultaneously, the duration and timing of maintenance, demand requirements, and the incompatibility of ertain pairs of units that should not be maintenance state in a week.
Libraries
To begin, we install and import the necessary libraries.
pip install quantagonia
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pulp import *
from quantagonia import HybridSolverParameters
import quantagonia.mip.pulp_adapter as pulp_adapter
Problem Parameters
NUM_UNITS: Number of units
NUM_WEEKS: Number of weeks
MAX_UNITS: Max units under maintenance simultaneously
MAINTENANCE_COSTS\(_{i}\): Maintenance Costs of Powerplant \(i\)
OPERATING_COSTS\(_{i}\): Operating Costs of Powerplant \(i\)
DEMANDS\(_{t}\): Demand of week \(t\)
OUTPUT_CAPACITIES\(_{i}\): Power Output Capacity of Powerplant \(i\)
DURATION_MAINTENANCE\(_{i}\): Duration of Maintenance of Powerplant \(i\)
INCOMPATIBLE_PAIRS: The Powerplant unit pairs that cannot be maintained together.
API_KEY = "Your-API-KEY" # if you don't have one, head over to https://platform.quantagonia.com/ (free account available)
# PARAMETERS
NUM_UNITS = 15 # Number of units
NUM_WEEKS = 15 # Number of weeks
MAX_UNITS = 4 # Max units under maintenance simultaneously
# Randomly Generated Parameters for Demonstration
np.random.seed(0)
MAINTENANCE_COSTS = np.random.randint(1000, 2000, size=(NUM_UNITS, NUM_WEEKS)) # Maintenance Costs
OPERATING_COSTS = np.random.randint(500, 1000, size=(NUM_UNITS, NUM_WEEKS)) # Operating Costs
DEMANDS = np.random.randint(25*NUM_UNITS, 75*NUM_UNITS, size=NUM_WEEKS) # Demand per period
OUTPUT_CAPACITIES = np.random.randint(50, 100, size=NUM_UNITS) # Power Output Capacity
DURATION_MAINTENANCE = np.random.randint(1, np.ceil(NUM_WEEKS/3), size=NUM_UNITS) # Duration of maintenance
## Incompatible pairs
## Randomly generate some powerplant unit pairs that cannot be maintained together
len_pairs = int(np.floor(NUM_UNITS/4))
INCOMPATIBLE_PAIRS = np.zeros((len_pairs,2),dtype=int)
for i in range(len_pairs):
random_units = np.random.choice(np.arange(0, NUM_UNITS), size=2, replace=False)
INCOMPATIBLE_PAIRS[i,0] = random_units[0]
INCOMPATIBLE_PAIRS[i,1] = random_units[1]
Sets and Indices
\(i \in U = {0,1,..,NumUnit}\) : Powerplant Indices
\(j \in W = {0,1,..,NumWeek}\) : Week Indices
# SETS
unitset = list(range(NUM_UNITS)) ## Unit Indices #i
weekset = list(range(NUM_WEEKS)) ## Week Indices #t
Decision Variables
\(x_{i, t} \in \{0, 1\}\): If unit i is ON for week t, it is 1; otherwise 0.
\(y_{i,t} \in \{0, 1\}\): If unit i is BEING MAINTAINED for week t, it is 1; otherwise 0.
#DECISION VARIABLES
### BINARY --> If unit i is ON for week t, it is 1; otherwise 0
x = []
for i in unitset:
x.append([])
for t in weekset:
x[i].append(LpVariable(name = 'isON(%d,%d)' % (i,t), cat='Binary'))
### BINARY --> If unit i is BEING MAINTAINED for week t, it is 1; otherwise 0
y = []
for i in unitset:
y.append([])
for t in weekset:
y[i].append(LpVariable(name = 'isMaintenance(%d,%d)' % (i,t), cat='Binary'))
Objective Function
The objective function is minimizing the total cost for the given planning horizon.
We calculate the total operational cost by summing the maintenance costs for each power plant unit that is under maintenance during a specific week, and by summing the operating costs for each power plant unit that is woking during a specific week.
prob = LpProblem("Maintenance_Scheduling", LpMinimize)
### OBJECTIVE FUNCTION
prob += lpSum(MAINTENANCE_COSTS[i,t]*y[i][t]
+ OPERATING_COSTS[i,t]*x[i][t] for i in unitset for t in weekset)
Constraints
Constraint 1:
Weekly power demand must be met.
Constraint 2:
Maintenance requirement must be met for the given horizon.
Constraint 3a:
Maintenance continuity constraint. If a unit begins maintenance in a week, it must remain under maintenance for consecutive weeks during its maintanence duration.
Constraint 3b:
Maintenance continuity constraint for the first week(t=0).
Constraint 4:
A Powerplant unit cannot be in Maintanance and Working state at the same time
Constraint 5:
Weekly maintenance of maximum units limitation constraint.
Constraint 6:
Incompatible pairs of powerplant units cannot be on maintenance state together.
### CONSTRAINTS
# Constraint 1: Power Demand Must Be Met
for t in weekset:
prob += (lpSum(OUTPUT_CAPACITIES[i] * x[i][t] for i in unitset) >= DEMANDS[t],
f"Constraint1_{t}")
# Constraint 2: Maintenance Requirement Must Be Met
for i in unitset:
prob += (lpSum(y[i][t] for t in weekset) == DURATION_MAINTENANCE[i],
f"Constraint2_{i}")
# Constraint 3a: Maintenance Continuity Constraint
for i in unitset:
for t in range(1,NUM_WEEKS-DURATION_MAINTENANCE[i]+1):
prob += (DURATION_MAINTENANCE[i]*(y[i][t] - y[i][t-1]) <=
lpSum(y[i][t2] for t2 in range(t,(t+DURATION_MAINTENANCE[i]))),
f"Constraint3a_{i,t}")
# Constraint 3b: Maintenance Continuity Constraint for the first week(t=0)
for i in unitset:
prob += (DURATION_MAINTENANCE[i]*(y[i][0]) <=
lpSum(y[i][t2] for t2 in range(0,(DURATION_MAINTENANCE[i]))),
f"Constraint3b_{i,0}")
# Constraint 4: A Unit cannot be in Maintanance and Working State at the Same Time
for i in unitset:
for t in weekset:
prob += (x[i][t] + y[i][t] <= 1, f"Constraint4_{i,t}")
# Constraint 5: Weekly Maintenance Max Unit Limit Constraint
for t in weekset:
prob += (lpSum(y[i][t] for i in unitset) <= MAX_UNITS,
f"Maintenance_Limit_Weekly_{t}")
# Constraint 6: Incompatible pairs cannot be maintained together
for (i1, i2) in INCOMPATIBLE_PAIRS:
for t in weekset:
prob += (y[i1][t] + y[i2][t] <= 1, f"Incompatible_Pairs_Unit_{i1}_{i2}_Week_{t}")
Defining Solver Parameters and Solve the Poblem
params = HybridSolverParameters()
params.set_time_limit(600)
params.set_seed(0)
q_solver = pulp_adapter.HybridSolver_CMD(api_key=API_KEY, params=params)
status = prob.solve(solver=q_solver)
print("Status:",LpStatus[status],"\nObjective Function Value: %.2f"%prob.objective.value())
✔ Queued job with jobid b97703f1-a038-45a0-9446-66a57b0c2439...
✔ Job b97703f1-a038-45a0-9446-66a57b0c2439 unqueued, processing...
Quantagonia HybridSolver version 1.1.1842
Copyright (c) 2024 Quantagonia GmbH.
User-specified parameters:
Set parameter 'time_limit' to value '600.0'.
Set parameter 'seed' to value '0'.
Read f8724d63cfc3482f85ce53bfcf7ad689-pulp.mps in 0.62s.
Minimize a MILP with 517 constraints and 450 variables (450 binary, 0 integer, 0 implied integer,0 continuous).
Presolving model. Presolved model in 0.0s.
Reduced model has 472 constraints and 450 variables (450 binary, 0 integer, 0 continuous).
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
1 | inf | 0.00000000 | inf | 0.00 |
* 1 | 153584.000 | 148184.339 | 3.52 | 0.01 |
* 1 | 153577.000 | 150081.172 | 2.28 | 0.02 |
* 1 | 152696.000 | 150426.702 | 1.49 | 0.03 |
* 7 | 152444.000 | 150441.042 | 1.31 | 0.09 |
* 61 | 152038.000 | 150441.042 | 1.05 | 0.43 |
* 77 | 151943.000 | 150441.042 | 0.99 | 0.55 |
* 95 | 151872.000 | 150495.423 | 0.91 | 0.67 |
* 201 | 151690.000 | 150944.157 | 0.49 | 1.24 |
* 278 | 151615.000 | 151330.124 | 0.19 | 1.47 |
* 304 | 151583.000 | 151569.533 | 0.01 | 1.54 |
------------------------------------------------------------------------
Optimal solution found (within relative tolerance 0.01%).
Solver Results:
- Solution Status: Optimal
- Wall Time: 1.5553 seconds
- Objective: 151583.000
- Bound: 151569.533
- Absolute Gap: 13.4672
- Relative Gap: 0.0089%
- Nodes: 304
- Best solution found at node 304 after 1.5397 seconds
Finished processing job b97703f1-a038-45a0-9446-66a57b0c2439...
Optimal
Status: Optimal
Objective Function Value: 151583.00
Creating the Outputs of the Solution
# Extract the isON and isMaintenance variable (x[i][t] and y[i][t])
resultx = np.zeros((NUM_UNITS,NUM_WEEKS))
resulty = np.zeros((NUM_UNITS,NUM_WEEKS))
maintenance_schedule_df = pd.DataFrame(columns = ['Powerplant_Id','Week_Id','Status'])
for i in unitset:
for t in weekset:
resultx[i,t]=int(round(x[i][t].varValue))
resulty[i,t]=int(round(y[i][t].varValue))
if resultx[i,t]>0.1:
new_row = ({'Powerplant_Id': int(i), 'Week_Id': int(t), 'Status': 'ON'})
maintenance_schedule_df = pd.concat([maintenance_schedule_df, pd.DataFrame([new_row])], ignore_index=True)
elif resulty[i,t]>0.1:
new_row = ({'Powerplant_Id': int(i), 'Week_Id': int(t), 'Status': 'MAINTENANCE'})
maintenance_schedule_df = pd.concat([maintenance_schedule_df, pd.DataFrame([new_row])], ignore_index=True)
else:
new_row = ({'Powerplant_Id': int(i), 'Week_Id': int(t), 'Status': 'OFF'})
maintenance_schedule_df = pd.concat([maintenance_schedule_df, pd.DataFrame([new_row])], ignore_index=True)
maintenance_schedule_df.sort_values(by=['Week_Id','Powerplant_Id'],inplace=True,ignore_index=True)
for i in unitset:
maintenance_schedule_df['Powerplant_Id']=maintenance_schedule_df['Powerplant_Id'].replace({i: 'Powerplant Unit '+str(i)})
for t in weekset:
maintenance_schedule_df['Week_Id']=maintenance_schedule_df['Week_Id'].replace({t: 'Week '+str(t)})
pivot_df = maintenance_schedule_df.pivot(index='Powerplant_Id', columns='Week_Id', values='Status')
order = list(range(NUM_WEEKS))
for i in range(NUM_WEEKS):
order[i] = 'Week ' + str(i)
pivot_df = pivot_df.reindex(columns=order)
power_df = pd.DataFrame(columns = ['Week_Id','Active_Powerplant','Maintenance_Powerplant','Inactive_Powerplant',
'Power_Demand','Power_Production'])
General Information About the Whole Powerplant
for t in weekset:
power_gen = int(np.sum(OUTPUT_CAPACITIES*resultx[:,t]))
new_row = ({'Week_Id': t, 'Active_Powerplant': int(np.sum(resultx[:,t])),
'Maintenance_Powerplant': int(np.sum(resulty[:,t])),
'Inactive_Powerplant': NUM_UNITS-int(np.sum(resultx[:,t]))-int(np.sum(resulty[:,t])),
'Power_Demand': DEMANDS[t], 'Power_Production': power_gen})
power_df = pd.concat([power_df, pd.DataFrame([new_row])], ignore_index=True)
power_df.set_index('Week_Id')
{"summary":"{\n \"name\": \"power_df\",\n \"rows\": 15,\n \"fields\": [\n {\n \"column\": \"Week_Id\",\n \"properties\": {\n \"dtype\": \"number\",\n \"std\": 4,\n \"min\": 0,\n \"max\": 14,\n \"num_unique_values\": 15,\n \"samples\": [\n 9,\n 11,\n 0\n ],\n \"semantic_type\": \"\",\n \"description\": \"\"\n }\n },\n {\n \"column\": \"Active_Powerplant\",\n \"properties\": {\n \"dtype\": \"date\",\n \"min\": 6,\n \"max\": 13,\n \"num_unique_values\": 7,\n \"samples\": [\n 10,\n 8,\n 13\n ],\n \"semantic_type\": \"\",\n \"description\": \"\"\n }\n },\n {\n \"column\": \"Maintenance_Powerplant\",\n \"properties\": {\n \"dtype\": \"date\",\n \"min\": 0,\n \"max\": 4,\n \"num_unique_values\": 5,\n \"samples\": [\n 2,\n 3,\n 4\n ],\n \"semantic_type\": \"\",\n \"description\": \"\"\n }\n },\n {\n \"column\": \"Inactive_Powerplant\",\n \"properties\": {\n \"dtype\": \"date\",\n \"min\": 0,\n \"max\": 6,\n \"num_unique_values\": 7,\n \"samples\": [\n 5,\n 3,\n 0\n ],\n \"semantic_type\": \"\",\n \"description\": \"\"\n }\n },\n {\n \"column\": \"Power_Demand\",\n \"properties\": {\n \"dtype\": \"date\",\n \"min\": 511,\n \"max\": 1028,\n \"num_unique_values\": 15,\n \"samples\": [\n 1028,\n 631,\n 845\n ],\n \"semantic_type\": \"\",\n \"description\": \"\"\n }\n },\n {\n \"column\": \"Power_Production\",\n \"properties\": {\n \"dtype\": \"date\",\n \"min\": 514,\n \"max\": 1061,\n \"num_unique_values\": 15,\n \"samples\": [\n 1033,\n 665,\n 850\n ],\n \"semantic_type\": \"\",\n \"description\": \"\"\n }\n }\n ]\n}","type":"dataframe"}
The Powerplant Unit Schedule
By shifting maintenance activities to weeks with lower power demand, the optimization model ensured that power supply remained stable and uninterrupted during peak demand times. Additionally, some of the power plants appear to be in mostly inactive state compared to others. These plants are the least efficient ones in terms of operating costs. Therefore, the optimization model that aims to minimize total costs uses these inefficient power plants primarily during periods of high demand.
from IPython.core.display import HTML
df_pivoted = pivot_df
# Define the function to map status to color
def status_to_color(status):
if status == 'ON':
return '#50C878'
elif status == 'OFF':
return '#000000' # '#990000'
elif status == 'MAINTENANCE':
return '#8C92AC'
return 'white'
# Create HTML table
html = """
<style>
.table-container {
width: 100%;
}
table {
border-collapse: collapse;
width: 100%;
}
th, td {
border: 1px solid black;
padding: 5px;
text-align: center;
}
.ellipse {
background-color: {};
border-radius: 50%;
width: 120px;
height: 40px;
display: flex;
align-items: center;
justify-content: center;
color: white;
font-weight: bold;
}
</style>
<div class='table-container'>
<table>
<tr><th>Powerplant_Id</th>"""
# Add week headers
for week in df_pivoted.columns:
html += f"<th>{week}</th>"
html += "</tr>"
# Add data rows
for i, row in df_pivoted.iterrows():
html += "<tr>"
html += f"<td>{i}</td>"
for col in df_pivoted.columns:
color = status_to_color(row[col])
html += f"<td><div class='ellipse' style='background-color: {color};'>{row[col]}</div></td>"
html += "</tr>"
html += "</table></div>"
# Display
HTML(html)
Powerplant_Id | Week 0 | Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | Week 6 | Week 7 | Week 8 | Week 9 | Week 10 | Week 11 | Week 12 | Week 13 | Week 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Powerplant Unit 0 | ON | OFF | ON | OFF | ON | OFF | ON | ON | ON | OFF | ON | OFF | OFF | MAINTENANCE | MAINTENANCE |
Powerplant Unit 1 | OFF | OFF | OFF | OFF | OFF | OFF | MAINTENANCE | MAINTENANCE | MAINTENANCE | ON | ON | OFF | OFF | OFF | OFF |
Powerplant Unit 10 | OFF | OFF | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE | ON | ON | ON | ON | ON | OFF | ON | ON | ON |
Powerplant Unit 11 | ON | OFF | ON | ON | ON | ON | ON | ON | ON | ON | ON | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE |
Powerplant Unit 12 | OFF | OFF | MAINTENANCE | MAINTENANCE | ON | ON | OFF | ON | OFF | ON | ON | ON | OFF | ON | ON |
Powerplant Unit 13 | ON | ON | ON | ON | ON | MAINTENANCE | ON | ON | ON | ON | ON | ON | ON | ON | ON |
Powerplant Unit 14 | ON | ON | ON | ON | ON | OFF | ON | ON | ON | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE | OFF | ON |
Powerplant Unit 2 | ON | ON | ON | ON | ON | ON | ON | ON | ON | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE | MAINTENANCE | ON |
Powerplant Unit 3 | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE | MAINTENANCE | ON | ON | OFF | ON | ON | ON | ON | ON | ON | ON |
Powerplant Unit 4 | ON | ON | ON | ON | ON | ON | MAINTENANCE | ON | ON | ON | ON | ON | ON | OFF | ON |
Powerplant Unit 5 | OFF | ON | ON | ON | ON | OFF | ON | ON | ON | ON | ON | ON | ON | OFF | MAINTENANCE |
Powerplant Unit 6 | OFF | ON | OFF | OFF | OFF | OFF | ON | ON | ON | ON | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE | OFF |
Powerplant Unit 7 | ON | MAINTENANCE | MAINTENANCE | ON | ON | ON | ON | ON | ON | ON | ON | ON | ON | ON | ON |
Powerplant Unit 8 | ON | ON | OFF | ON | ON | ON | ON | ON | MAINTENANCE | MAINTENANCE | MAINTENANCE | MAINTENANCE | OFF | ON | ON |
Powerplant Unit 9 | ON | ON | MAINTENANCE | MAINTENANCE | ON | OFF | ON | ON | ON | ON | ON | ON | OFF | ON | ON |
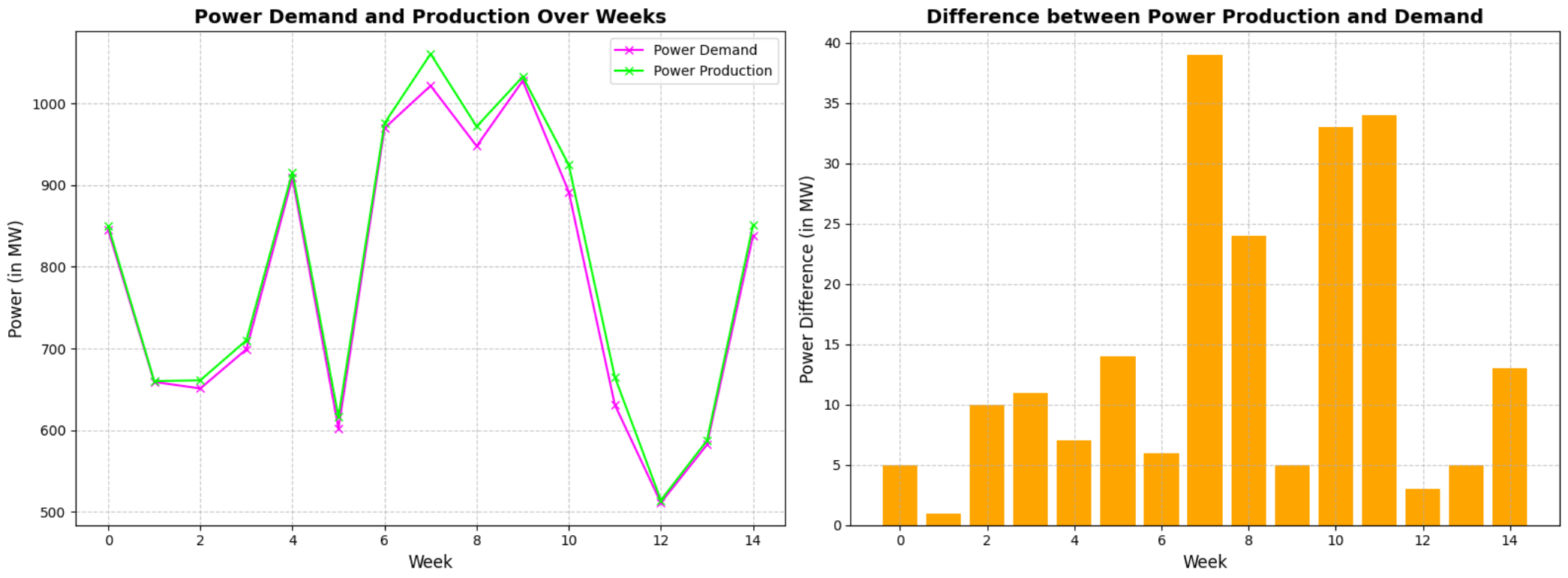
Power Production vs. Demand
power_df['Power_Difference'] = power_df['Power_Production']-power_df['Power_Demand']
fig, axs = plt.subplots(1, 2, figsize=(16, 6))
# Plot 1: Power Demand and Production over Weeks
axs[0].plot(power_df['Week_Id'], power_df['Power_Demand'], label='Power Demand', color='magenta', marker='x')
axs[0].plot(power_df['Week_Id'], power_df['Power_Production'], label='Power Production', color='lime', marker='x')
axs[0].set_title('Power Demand and Production Over Weeks', fontsize=14, fontweight='bold')
axs[0].set_xlabel('Week', fontsize=12)
axs[0].set_ylabel('Power (in MW)', fontsize=12)
axs[0].legend()
axs[0].grid(True, linestyle='--', alpha=0.7)
#axs[0].set_facecolor('#e6f7ff')
# Plot 2: Difference between Power Production and Demand
axs[1].bar(power_df['Week_Id'], power_df['Power_Difference'], color='orange')
axs[1].set_title('Difference between Power Production and Demand', fontsize=14, fontweight='bold')
axs[1].set_xlabel('Week', fontsize=12)
axs[1].set_ylabel('Power Difference (in MW)', fontsize=12)
axs[1].grid(True, linestyle='--', alpha=0.7)
#axs[1].set_facecolor('#e6f7ff')
plt.tight_layout()
plt.show()
It can be seen that power demand fluctuated over the weeks, with notable peaks and troughs.
Power production generally aligned with demand, but there were periods where production slightly exceeded the demand. This is expected because small adjustments on the power production of the units is not possible for our case, and power plant units have to produce a fixed amount of energy within a certain period. Additionally, the excess power production is at its minimal rate when compared to the total power production.
Lastly, there is no power shortage during the horizon thanks to demand constraint being a hard constraint.
Conclusion
This case demonstrates that through careful analysis and strategic scheduling, power production can be optimized to meet demand requirements while ensuring critical maintenance activities are performed. This approach ensures a stable power supply, improves operational efficiency, and enhances the overall reliability of the power plant.
Need help with modeling? We are happy to coach you through your model formulation. Reach out to us at help@quantagonia.com or https://www.quantagonia.com/contact.
## References
Frost, D., Dechter, R. Maintenance scheduling problems as benchmarks for constraint algorithms. Annals of Mathematics and Artificial Intelligence 26, 149–170 (1999). https://doi.org/10.1023/A:1018906911996