The Drone Delivery Problem#
Optimization Model for Drone Delivery
This notebooks outlines the optimization model designed to determine the minimum distance for drone delivery routing problems. The model employs a Mixed Integer Linear Programming (MILP) approach to minimize the total travel distance required to deliver packages from a warehouse to various delivery points.
Libraries
To begin, we import the necessary libraries.
pip install quantagonia
pip install folium
API_KEY="Your-API-KEY" # if you don't have one, head over to https://platform.quantagonia.com/ (free account available)
import numpy as np
import pandas as pd
import time as ttt
import random
import math
import folium
from pulp import *
from quantagonia import HybridSolverParameters
import quantagonia.mip.pulp_adapter as pulp_adapter
# Define problem parameters
NUM_LOCATIONS = 12 # Number of Location Points Including Warehouse
DRONE_CAPACITY = 3
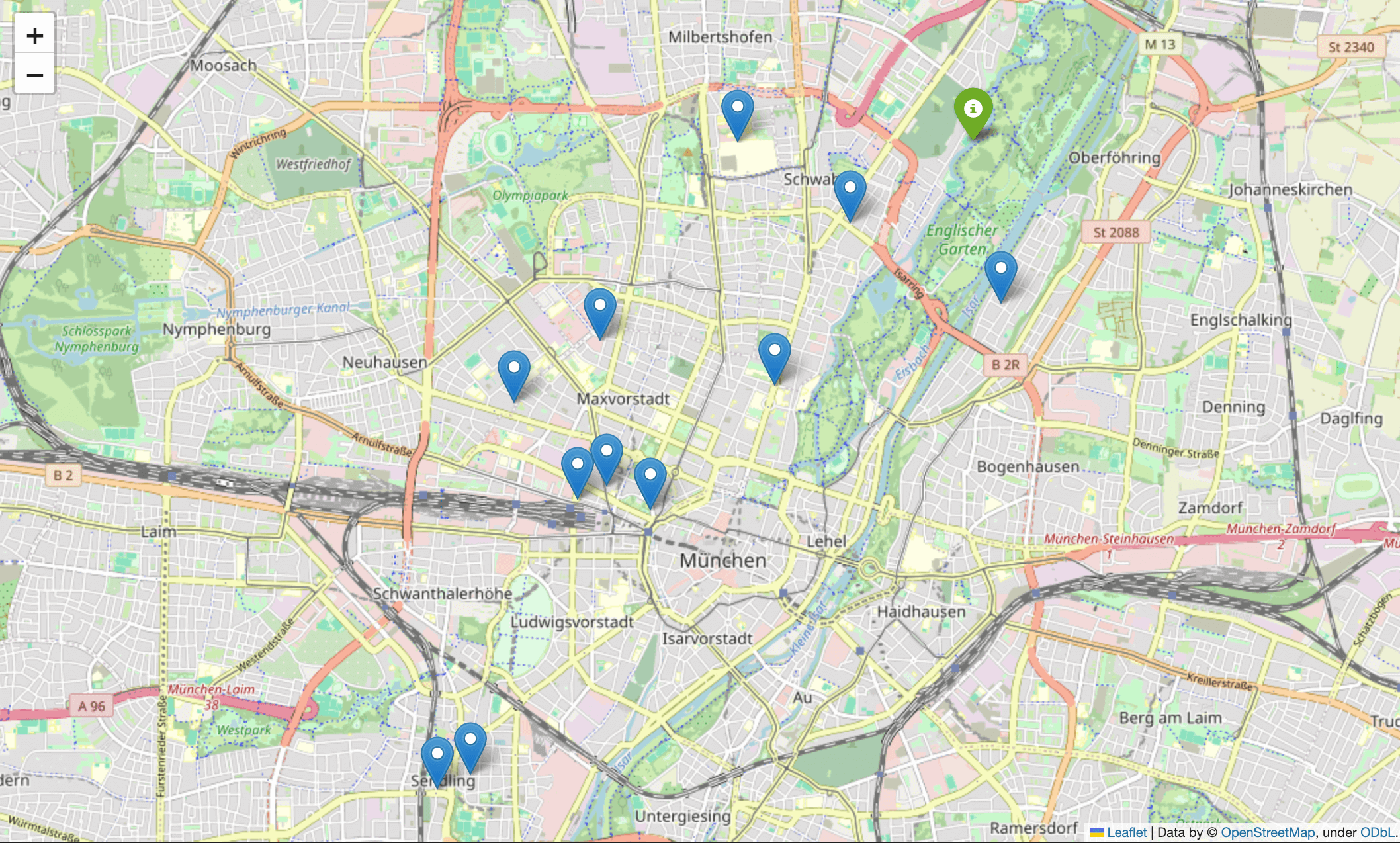
Generate coordinates for the selected area, which in our case is Munich. To gain an initial perspective on our problem, we will visualize the data using the Folium.
random.seed(2)
# Latitude and Longitude ranges for Munich
lat_range = (48.114972911995785, 48.17622969284977) # Approximate latitude range for Munich
lon_range = (11.536111191947134, 11.611750294370422) # Approximate longitude range for Munich
# Generate random coordinates within the specified range
coordinates=np.zeros(NUM_LOCATIONS,dtype=object)
for i in range(NUM_LOCATIONS):
coordinates[i] = (round(random.uniform(lat_range[0], lat_range[1]), 17), round(random.uniform(lon_range[0], lon_range[1]), 8))
# Create a map centered around the average coordinates
avg_lat = sum(lat for lat, lon in coordinates) / len(coordinates)
avg_lon = sum(lon for lat, lon in coordinates) / len(coordinates)
map_munich = folium.Map(location=[avg_lat, avg_lon], zoom_start=10)
# Add markers for each coordinate
for i, coord in enumerate(coordinates):
if i == 0:
folium.Marker(location=coord, popup=f"Name: Warehouse, Lat: {coord[0]}, Lon: {coord[1]}", icon=folium.Icon(color='green')).add_to(map_munich)
else:
folium.Marker(location=coord, popup=f"Name: Delivery Point {i}, Lat: {coord[0]}, Lon: {coord[1]}").add_to(map_munich)
# Save the map to an HTML file
map_munich.save("Munich_coordinates_map.html")
# If running in a Jupyter notebook, display the map
map_munich
Distance Calculation
We use the Haversine formula to calculate the distance between two geographic coordinates and then construct the distance matrix for the model.
# Haversine Distance Function
def haversine_distance(coord1, coord2):
R = 6371 # Radius of the Earth in kilometers
lat1, lon1 = math.radians(coord1[0]), math.radians(coord1[1])
lat2, lon2 = math.radians(coord2[0]), math.radians(coord2[1])
dlat = lat2 - lat1
dlon = lon2 - lon1
a = math.sin(dlat / 2)**2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2)**2
c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
return R * c
# Construct the distance matrix
distance_matrix = np.zeros((len(coordinates),len(coordinates)))
for i in range(len(coordinates)):
for j in range(len(coordinates)):
distance_matrix[i,j] = haversine_distance(coordinates[i], coordinates[j])
Sets and Indices:
Now, we define the sets:
\(i,j \in \text{locationset} = \{0,1,\ldots,(n-1)\}\), the set of locations (including warehouse, \(idx=0\))
\(i,j \in \text{locationset_without_wh} = \{1,2,\ldots,(n-1)\}\), the set of locations (excluding warehouse, \(idx=0\))
\(t \in \text{tours} = \{0,1,\ldots,\text{Maximum_Tours}\}\), the set of tours
# SETS
locationset = list(range(NUM_LOCATIONS)) ## Location set includinng warehouse (idx=0)
locationset_without_wh = list(range(1,NUM_LOCATIONS)) ## Location set excluding warehouse (idx=0)
tours = list(range(math.ceil((NUM_LOCATIONS-1)/DRONE_CAPACITY))) ## Tour set
Decision Variables
We define the decision variables for the model to be:
\(x_{ijt}\): binary Variable, 1 if location \(j\) is visited after location \(i\) within tour \(t\), otherwise 0.
\(y_{it}\): binary Variable, 1 if location \(i\) is visited in tour \(t\), otherwise \(0\).
\(u_i\): auxiliary integer variable to eliminate subtours, representing the order in which delivery point \(i\) is visited.
#DECISION VARIABLES
### x[i][j][t] - Binary: if location j is visited after location i within tour t, then 1; otherwise 0
x = []
for i in locationset:
x.append([])
for j in locationset:
x[i].append([])
for t in tours:
x[i][j].append(LpVariable(name = 'x(%d,%d,%d)' % (i,j,t), cat='Binary'))
### y[i][t] - Binary: if location i is visited in tour t, then 1; otherwise 0
y = []
for i in locationset:
y.append([])
for t in tours:
y[i].append(LpVariable(name = 'y(%d,%d)' % (i,t), cat='Binary'))
### u[i] - Auxiliary variable to eliminate subtours, representing the order in which delivery point i is visited
u = []
for i in locationset:
u.append(LpVariable(name = 'u(%d)' % (i),lowBound=0, cat='Integer'))
Objective Function
We define the objective function to minimize the total travel distance:
\begin{equation} \text{Minimize} \quad Z = \sum_{i \in \text{locationset}} \sum_{j \in \text{locationset}} \sum_{t \in \text{tours}} x_{ijt} \cdot \text{distance_matrix}_{ij} \tag{0} \end{equation}
Z = LpProblem("Deliver_Packages", LpMinimize)
### OBJECTIVE FUNCTION
Z += lpSum(x[i][j][t]*distance_matrix[i][j] for i in locationset for j in locationset for t in tours)
Constraints
Constraint 1:
The number of entries and exits for each location must be the same.
\[\begin{split}\begin{align}
\sum_{i \in \text{locationset}} x_{ijt} &= \sum_{i \in \text{locationset}} x_{jit}, \quad \forall j \in \text{locationset}, \forall t \in \text{tours}
\tag{1}\\
\end{align}\end{split}\]
Constraint 2a:
The number of entries to each location \(j\) must be equal to 1 if it is visited in tour \(t\).
\[\begin{split}\begin{align}
\sum_{i \in \text{locationset}, i \neq j} x_{ijt} &= y_{jt}, \quad \forall j \in \text{locationset}, \forall t \in \text{tours}
\tag{2a}\\
\end{align}\end{split}\]
Constraint 2b:
The number of departures from each location \(i\) must be equal to 1 if it is visited in tour \(t\).
\[\begin{split}\begin{align}
\sum_{j \in \text{locationset}, j \neq i} x_{ijt} &= y_{it}, \quad \forall i \in \text{locationset}, \forall t \in \text{tours}
\tag{2b}\\
\end{align}\end{split}\]
Constraint 3:
Each delivery location must be visited.
\[\begin{split}\begin{align}
\sum_{t \in \text{tours}} y_{it} &= 1, \quad \forall i \in \text{locationset_without_wh}
\tag{3}\\
\end{align}\end{split}\]
Constraint 4:
Capacity constraint: The maximum number of customers visited is limited by the drone’s capacity. Additionally, the warehouse node must be visited if any tour is activated.
\[\begin{split}\begin{align}
\sum_{i \in \text{locationset_without_wh}} y_{it} &\leq \text{DRONE_CAPACITY}*y_{0t}, \quad \forall t \in \text{tours}
\tag{4}\\
\end{align}\end{split}\]
Constraint 5a:
Subtour elimination and order constraints (Miller-Tucker-Zemlin (MTZ) formulation).
\[\begin{split}\begin{align}
u_i - u_j + \text{DRONE_CAPACITY} \cdot x_{ijt} &\leq \text{DRONE_CAPACITY} - 1, \quad \forall i, j \in \text{locationset_without_wh}, i \neq j, \forall t \in \text{tours}
\tag{6a}\\
\end{align}\end{split}\]
Constraint 5b:
Subtour elimination and order constraints (MTZ formulation).
\[\begin{split}\begin{align}
1 \leq u_i &\leq \text{DRONE_CAPACITY}, \quad \forall i \in \text{locationset_without_wh}
\tag{6b}\\
\end{align}\end{split}\]
### CONSTRAINTS
# Constraint 1: The number of entries and exits for each location must be the same.
for j in locationset:
for t in tours:
Z += lpSum(x[i][j][t] for i in locationset) == lpSum(x[j][i][t] for i in locationset)
# Constraint 2a: The number of entries to each location j must be equal to 1 if it is visited in tour t.
for j in locationset:
for t in tours:
Z +=lpSum(x[i][j][t] for i in locationset if i!=j) == y[j][t]
# Constraint 2b: The number of departures from each location i must be equal to 1 if it is visited in tour t.
for i in locationset:
for t in tours:
Z +=lpSum(x[i][j][t] for j in locationset if j!=i) == y[i][t]
# Constraint 3: Each delivery location must be visited.
for i in locationset_without_wh:
Z += lpSum(y[i][t] for t in tours) == 1
# Constraint 4: Capacity constraint: The maximum number of customers visited is limited by the drone's capacity.
# Additionally, the warehouse node must be visited if any tour is activated.
for t in tours:
Z += lpSum(y[i][t] for i in locationset_without_wh) <= DRONE_CAPACITY*y[0][t]
# Constraint 5a: Subtour Elimination and Order Constraints (Miller-Tucker-Zemlin (MTZ) formulation).
for t in tours:
for i in locationset_without_wh:
for j in locationset_without_wh:
if i==j:
continue
Z += (u[i]-u[j]+DRONE_CAPACITY*x[i][j][t] <= DRONE_CAPACITY-1)
# Constraint 5b: Subtour Elimination and Order Constraints (MTZ formulation).
for t in tours:
for i in locationset_without_wh:
Z += (u[i] <= DRONE_CAPACITY)
Z += (u[i] >= 1)
Solving the Model
We define the parameters (e.g. Time, Gap) and solve the model using a the HybridSolver from Quantagonia.
params = HybridSolverParameters()
params.set_time_limit(600)
params.set_seed(0)
q_solver = pulp_adapter.HybridSolver_CMD(api_key=API_KEY, params=params)
status = Z.solve(solver=q_solver)
print("Status:",LpStatus[status],"\nObjective Function Value: %.2f"%Z.objective.value(),"km")
✔ Queued job with jobid 0028b7fb-9985-4f49-a3dc-f18e118b3b0a...
✔ Job 0028b7fb-9985-4f49-a3dc-f18e118b3b0a unqueued, processing...
Quantagonia HybridSolver version 1.1.1781
Copyright (c) 2024 Quantagonia GmbH.
User-specified parameters:
Set parameter 'time_limit' to value '600.0'.
Set parameter 'seed' to value '0'.
Read b145cc629f4d4258ae4d044a766029be-pulp.mps in 0.59s.
Minimize a MILP with 687 constraints and 635 variables (624 binary, 11 integer, 0 implied integer,0 continuous).
Presolving model. Presolved model in 0.0s.
Reduced model has 551 constraints and 576 variables (565 binary, 11 integer, 0 continuous).
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
1 | inf | 0.00000000 | inf | 0.00 |
* 1 | 46.7744772 | 19.8227293 | 57.62 | 0.00 |
* 3 | 43.9381887 | 27.2419397 | 38.00 | 0.02 |
* 59 | 43.3015915 | 27.2488165 | 37.07 | 0.43 |
* 82 | 43.0262083 | 27.2488165 | 36.67 | 0.68 |
* 162 | 42.3020208 | 27.2496758 | 35.58 | 1.27 |
* 229 | 42.1412607 | 27.2605539 | 35.31 | 1.80 |
386 | 42.1412607 | 27.2622454 | 35.31 | 2.93 |
* 539 | 42.1061606 | 27.2622454 | 35.25 | 4.23 |
* 880 | 41.9052291 | 28.0060363 | 33.17 | 4.76 |
* 884 | 41.8789535 | 28.0060363 | 33.13 | 4.86 |
* 1131 | 41.7559333 | 29.8798681 | 28.44 | 5.69 |
2017 | 41.7559333 | 31.0858794 | 25.55 | 11.48 |
2142 | 41.7559333 | 31.4118209 | 24.77 | 12.80 |
2338 | 41.7559333 | 31.6075000 | 24.30 | 14.04 |
2521 | 41.7559333 | 31.6556399 | 24.19 | 15.06 |
2770 | 41.7559333 | 32.1571995 | 22.99 | 16.10 |
2878 | 41.7559333 | 32.4013208 | 22.40 | 17.15 |
3036 | 41.7559333 | 32.6622455 | 21.78 | 18.62 |
3249 | 41.7559333 | 32.7038099 | 21.68 | 19.90 |
3465 | 41.7559333 | 32.8898708 | 21.23 | 21.54 |
3682 | 41.7559333 | 32.9232617 | 21.15 | 22.86 |
3908 | 41.7559333 | 33.0918351 | 20.75 | 24.07 |
4073 | 41.7559333 | 33.2434330 | 20.39 | 25.97 |
4385 | 41.7559333 | 33.3867754 | 20.04 | 27.48 |
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
5280 | 41.7559333 | 33.5461010 | 19.66 | 28.54 |
5425 | 41.7559333 | 33.7102887 | 19.27 | 29.89 |
5811 | 41.7559333 | 33.7967712 | 19.06 | 31.01 |
6093 | 41.7559333 | 33.8393989 | 18.96 | 32.40 |
6491 | 41.7559333 | 34.0827942 | 18.38 | 33.42 |
6590 | 41.7559333 | 34.2933256 | 17.87 | 34.68 |
6883 | 41.7559333 | 34.4214993 | 17.57 | 35.74 |
7370 | 41.7559333 | 34.6465789 | 17.03 | 37.63 |
7620 | 41.7559333 | 34.8405817 | 16.56 | 38.85 |
8069 | 41.7559333 | 34.9895971 | 16.20 | 40.07 |
8380 | 41.7559333 | 35.1596993 | 15.80 | 41.13 |
8557 | 41.7559333 | 35.5214184 | 14.93 | 42.23 |
8926 | 41.7559333 | 35.6900359 | 14.53 | 43.50 |
9366 | 41.7559333 | 35.8195714 | 14.22 | 44.66 |
9814 | 41.7559333 | 35.8797123 | 14.07 | 45.72 |
10041 | 41.7559333 | 36.0815336 | 13.59 | 46.83 |
10391 | 41.7559333 | 36.3871303 | 12.86 | 48.00 |
10626 | 41.7559333 | 36.5415914 | 12.49 | 49.02 |
10924 | 41.7559333 | 36.7241490 | 12.05 | 50.25 |
11593 | 41.7559333 | 36.9130140 | 11.60 | 51.30 |
11826 | 41.7559333 | 37.0363145 | 11.30 | 52.47 |
12032 | 41.7559333 | 37.1233716 | 11.09 | 53.69 |
12624 | 41.7559333 | 37.4367840 | 10.34 | 55.43 |
13483 | 41.7559333 | 37.6922509 | 9.73 | 56.55 |
13823 | 41.7559333 | 37.9103551 | 9.21 | 57.75 |
------------------------------------------------------------------------
Nodes | Incumbent | Bound | Gap (%) | Time (s) |
------------------------------------------------------------------------
14282 | 41.7559333 | 38.2179958 | 8.47 | 58.94 |
14597 | 41.7559333 | 38.4545453 | 7.91 | 59.95 |
14974 | 41.7559333 | 38.6770731 | 7.37 | 60.99 |
15903 | 41.7559333 | 38.9883507 | 6.63 | 62.13 |
16327 | 41.7559333 | 39.2174342 | 6.08 | 63.20 |
16788 | 41.7559333 | 39.4652921 | 5.49 | 64.27 |
17336 | 41.7559333 | 39.7677276 | 4.76 | 65.38 |
18056 | 41.7559333 | 40.2870297 | 3.52 | 66.44 |
18918 | 41.7559333 | 41.7534278 | 0.01 | 67.44 |
------------------------------------------------------------------------
Optimal solution found (within relative tolerance 0.01%).
Solver Results:
- Solution Status: Optimal
- Wall Time: 67.4439 seconds
- Objective: 41.7559333
- Bound: 41.7534278
- Absolute Gap: 0.0025
- Relative Gap: 0.006%
- Nodes: 18918
- Best solution found at node 1131 after 6.2713 seconds
Finished processing job 0028b7fb-9985-4f49-a3dc-f18e118b3b0a...
Optimal
Status: Optimal
Objective Function Value: 41.76 km
Results
We extract the results:
# GET THE END RESULTS OF THE VARIABLES
resultx = np.zeros((len(locationset),len(locationset),len(tours)))
for i in locationset:
for j in locationset:
for t in tours:
resultx[i,j,t] = x[i][j][t].varValue
resulty = np.zeros((len(locationset),len(tours)))
for i in locationset:
for t in tours:
resulty[i,t] = y[i][t].varValue
## Extract the sequences
result_u = np.zeros(len(locationset))
for i in locationset_without_wh:
result_u[i]=u[i].varValue
## Extract the squences of the locations and which in tour they are visited
sequence_tour = np.zeros((NUM_LOCATIONS,2))
sequence_tour[:,1] = -1
for i in locationset_without_wh:
sequence_tour[i,0] = int(round(result_u[i]))
for t in tours:
if int(round(resulty[i,t]))==1:
sequence_tour[i,1] = t
# Construct the Output DataFrame
output_df = pd.DataFrame(sequence_tour[1:], columns=['Sequence','Tour'])
output_df['Location_Index'] = range(1,len(sequence_tour))
output_df['Coordinates'] = coordinates[1:]
output_df.sort_values(['Tour', 'Sequence'], ascending=[True, True],inplace=True)
for i in range(1,len(output_df)):
if output_df.iloc[i,1] == output_df.iloc[i-1,1]:
output_df.iloc[i,0] = output_df.iloc[i-1,0] + 1
else:
output_df.iloc[i,0] = 1
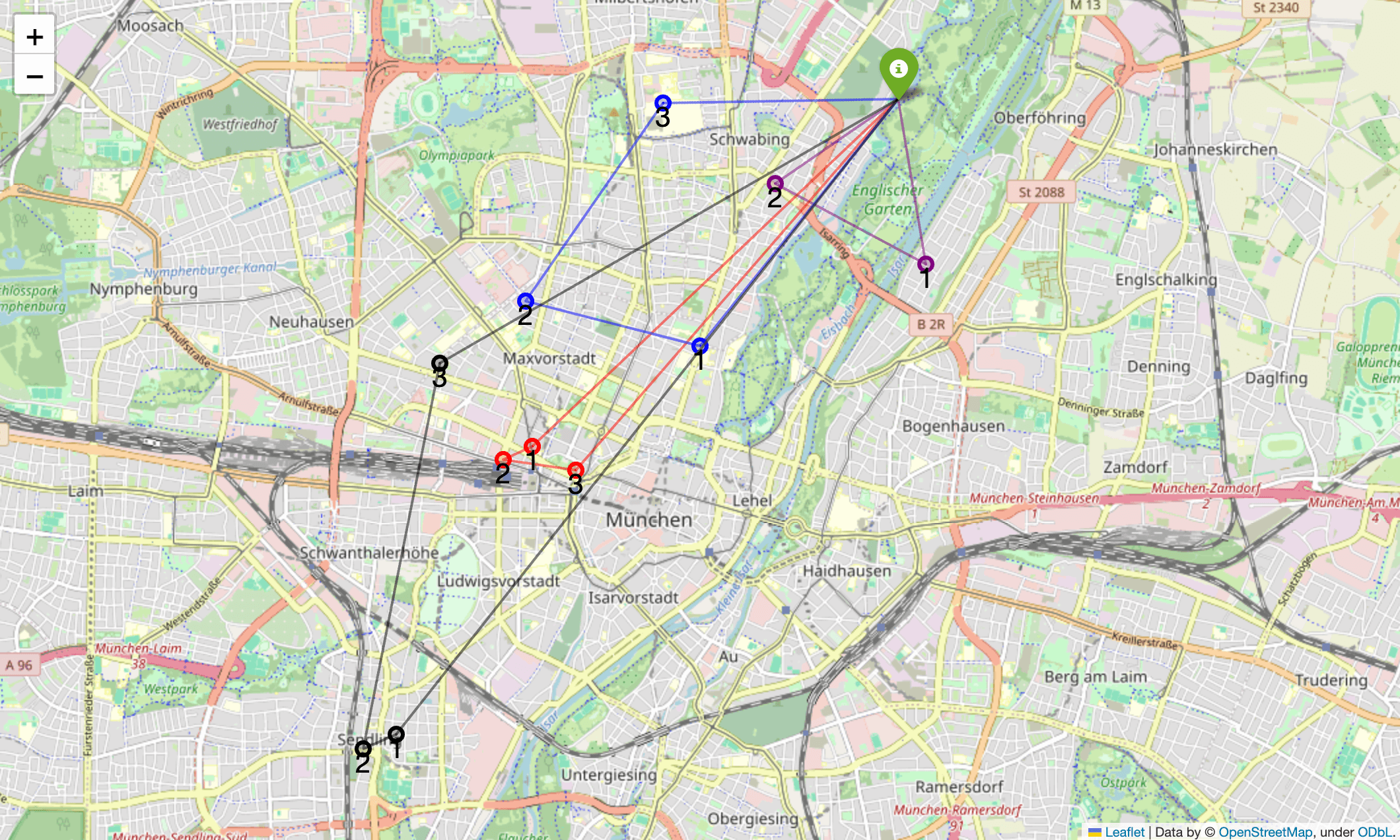
Visualizing the Results
We visualize the results using Folium:
### MAP VIEW OF THE SOLUTION
# Define the list of colors for the tours (currently max tours is limited by 15)
colors = ['purple', 'red', 'blue', 'black', 'darkred', 'lightred', 'beige',
'darkblue', 'cadetblue', 'darkpurple', 'pink', 'lightblue',
'gray', 'orange', 'lightgray']
# Calculate the average coordinates for centering the map
avg_lat = sum(lat for lat, lon in coordinates) / len(coordinates)
avg_lon = sum(lon for lat, lon in coordinates) / len(coordinates)
# Create a map centered around the average coordinates
map_munich = folium.Map(location=[avg_lat, avg_lon], zoom_start=10)
# Add the first marker as the warehouse with a green icon
folium.Marker(
location=coordinates[0],
popup=f"Name: Warehouse, Lat: {coordinates[0][0]}, Lon: {coordinates[0][1]}",
icon=folium.Icon(color='green')).add_to(map_munich)
# Add markers for each coordinate
for i in range(len(output_df)):
# Add markers for other locations with DivIcon displaying the sequence number
folium.Marker(
location=output_df['Coordinates'].iloc[i],
popup=f"Location {output_df['Location_Index'].iloc[i]}: Lat: {output_df['Coordinates'].iloc[i][0]}, Lon: {output_df['Coordinates'].iloc[i][1]}",
icon=folium.DivIcon(html=f'<div style="font-size: 16pt; color : black">{int(output_df["Sequence"].iloc[i])}</div>')
).add_to(map_munich)
# Add circle markers for other locations with specified colors
folium.CircleMarker(
location=output_df['Coordinates'].iloc[i],
radius=5,
color=colors[int(output_df['Tour'].iloc[i])%len(colors)],
fill=True,
fill_color=colors[int(output_df['Tour'].iloc[i])%len(colors)]
).add_to(map_munich)
# Create a dictionary to store coordinates by tour
tour_coordinates = {}
for i in range(len(output_df)):
tour = output_df['Tour'].iloc[i]
if tour not in tour_coordinates:
tour_coordinates[tour] = []
tour_coordinates[tour].append(output_df['Coordinates'].iloc[i])
# Draw dashed lines for each tour
for tour, coords in tour_coordinates.items():
# Connect warehouse to the first location in the tour
folium.PolyLine(
locations=[coordinates[0], coords[0]],
color=colors[int(tour)%len(colors)],
weight=2,
opacity=0.5,
dash_array='1, 1'
).add_to(map_munich)
# Connect each location in the tour by its sequence
folium.PolyLine(
locations=coords,
color=colors[int(tour)%len(colors)],
weight=2,
opacity=0.5,
dash_array='1, 1'
).add_to(map_munich)
# Connect the last location in a tour back to the warehouse
folium.PolyLine(
locations=[coords[-1], coordinates[0]],
color=colors[int(tour)%len(colors)],
weight=2,
opacity=0.5,
dash_array='1, 1'
).add_to(map_munich)
map_munich.save("map_munich.html")
map_munich
Need help with modeling? We are happy to coach you through your model formulation. Reach out to us at help@quantagonia.com or https://www.quantagonia.com/contact.